DIY functional oscillators

 

Signal distortion induced by electronic devices, primarily amplifiers, could be either undesirable or useful.

When we play back an audio recording, we want it to sound as close to the original as possible. Or sometimes, we want to add just a smidge of tube distortion.

On the other hand, magnetic recording on tape and mechanical recording on vinyl, by their nature, significantly alter the sound; therefore, distortions are deliberately added into the circuits of recorders and playback equipment so that, in the end, the resulting audio signal turns out to be indistinguishable from what has been recorded.

In addition, volume controls are equipped with loudness compensation to account for human hearing abilities.

Mobile pocket audio devices have tiny speakers, and their power amplifiers are specifically designed to add bass and limit treble so that the sound is deeper and less squeaky.

Multi-way speaker systems have filters, and sometimes even separate amplifiers, that slice the sound signal into frequency bands for each dedicated speaker: subwoofer, low-frequency, mid-frequency, and tweeter. These can also be considered deliberately created distortions.

Finally, processing an electric guitar signal requires numerous fine-tuned distortions. They form a wonderful guitar tone. But if we simply plug the best electric guitar into a hi-fi amplifier, we'll be disappointed.

One can also identify a malfunction by the specific distortions of the signal and, by tracking the signal flow, specify the location of the malfunction in a complex circuit.

A device that allows you to see distortions is called an oscilloscope. But having an oscilloscope is not enough; we will also need a standard waveform signal generator. Today, we will assemble three such generators.

So-called standard waveforms are sine, triangle, and square. Devices that generate such signals are called function generators.

A sine wave is the simplest signal, but it is the most difficult to create without an LC resonant tank, using only RC circuits. A pure sine wave oscillates one frequency; it is needed to determine the harmonics the circuit adds to the signal.

For example, in this image from the post about the tube amplifier, we see that the upper half-wave is wide and rounded, and the lower half-wave is narrow and pointy. This indicates the presence of a second harmonic, which makes tube amplifiers sound so beautiful.

A triangular waveform could be created by a ramp voltage generator. Such a signal allows one to see nonlinear distortions as lines bend on the oscilloscope screen.

Bending them a certain way brings the triangle line closer to a sinusoid. This is exactly how the function generators on microchips that we are studying today are designed.

An ideal square wave consists of vertical and horizontal lines. Looking at the flow of such a signal, one can see the frequency-dependent deviations, interference, and parasitic processes.

For example, a differentiating circuit with a time constant of an order of magnitude smaller than the period of the input signal creates a sharp peak at the beginning of the horizontal section.

And this is what the result of the operation of an integrating circuit with a time constant comparable to the signal period looks like.

If the integrator time constant is noticeably smaller than the signal period, then only the leading edges become sloped, and the top part of the square wave remains flat. In this oscillogram, we see additional high-frequency interference.

Here, we see not just high-frequency noise but damping oscillations excited by sudden changes in the input signal. Such vibrations are called "ringing".

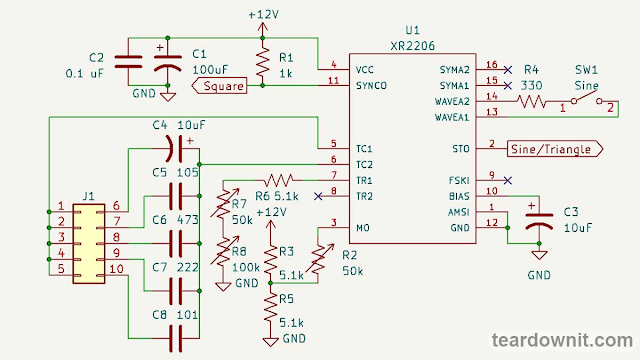
Function generator on the XR2206 chip

Our first generator can produce electrical oscillations with frequencies ranging from 1 Hz to 1 MHz. This is more than enough for an amateur's lab.

The 300 kHz square wave we have here is distorted not by the generator itself but by the DSO112A oscilloscope, whose analog bandwidth is 2 MHz.

At 20 kHz, the upper limit of the audible range, the square waveform appears almost perfect.

The generator volume knob allows one to crank it up to the limiter. This generator feature must be kept in mind, or the limitation may sometimes seem to occur in the circuit under study.

The 400 kHz sine wave looks great. Remember that this is 1/5 of the oscilloscope's bandwidth, so all the harmonics higher than the fifth won't pass through the oscilloscope's analog input.

This is a triangular waveform at a frequency of 130 kHz. The tops are slightly rounded, but the lines are straight. Everything looks as it should.

The generator circuit is elementary. Capacitors C1 and C2 together are a power filter. The square wave output is pulled up by resistor R1 to the power supply positive because it is an open collector output.

 

C4-C8 are timing capacitors, and J1 is their frequency range switch.

Timing resistance is made up of three series resistors. R8 is a coarse frequency setting, R7 is a fine setting, and R6 is a limiting resistor, so it cannot be zero.

The circuit has input 8 (TR2) for the second timing resistor. Pull pin 9 (FSKI) to the ground; input 8 (TR2) will become active. If input 8 is left disconnected or pulled to the power supply positive, then input 7 (TR1) is active.

This option allows one to instantly switch between two oscillation periods, which is helpful for frequency shift keying or pulse width modulation.

To get PWM, one needs to connect input 9 (FSKI) to output 11 (SYNCO). Then, the duty cycle will be determined by the ratio of the resistances connecting TR1 and TR2 to the ground, and the frequency will be determined by the sum of these resistances.

Pin 3 (MO) bias setting is the gain adjustment. It is the amplitude of the output signal and is tweaked with a variable resistor, R2.

Pins 13 and 14 (WAVEA1, WAVEA2) are used to form a sinusoid. Output 2 (STO) produces a triangle waveform if they are open. If those pins are connected through a resistor, there will be a sine wave. Its shape can be adjusted by changing the resistance R4.

Input 1 (AMSI) is intended for amplitude modulation. We don't use it in this scheme.

Output 10 (BIAS) is connected to the internal reference voltage source. To ensure its stability and the absence of any interference, a capacitor C3 is connected to it.

You can add a potentiometer to pins 15 and 16 (SYMA1 and SYMA2) and connect its wiper to the ground. Then, it will be possible to further adjust the symmetry of the sinusoid. Although, as we've seen, this is optional.

Function generator on the ICL8038 chip

The ICL8038 chip has much in common with the XR2206; it is also designed to create a function generator with minimum external components.

Like the XR2206, the ICL8038 has a timing capacitor on input 9 (TIME_CAP). We switch through five different capacitors to get five frequency ranges.

Square wave output 9 (SQR_OUT) for both microcircuits is an open collector. It needs to be pulled up to the positive power supply. ICL8038 has separate sine and triangle outputs: 2 (SINE_OUT) and 3 (TRI_OUT).

The ICL8038 has only one input for timing resistor 8 (FM SWEEP), so we won't be able to switch between resistors and get FSK.

But inputs 4 and 5 allow one to adjust the duty cycle of PWM. The resistances between these pins and the power supply positive, set by the position of wiper RV2, affect all three outputs.

Resistor RV4, the bias of input 1 (SINE_ADJ), tweaks the vertical symmetry of the sine wave. As we already know, this affects the harmonic series of the signal.

Simple function generator on NE555

If you do not have a specialized chip, a simple square, triangle, and sine wave generator can be assembled in many ways, for example, on a 555 timer.

We see an emitter follower on transistor Q1 at the device's output. It has a positive bias in the form of resistor R10. The input resistance of this stage is about 100 kOhm, so the voltage at the base of Q1 will be about half the supply voltage.

In the first position of the switch, rectangular pulses from the output of the 555 timers pass through series capacitors C4 and C5 and parallel capacitor C6. Resistor R3 is connected with C4, and R4 is connected in parallel with C6.

The result is a hybrid of a rectangle and a ramp with decent linearity. One can evaluate the distortion and parasitic oscillations it introduces by comparing the original waveform with what is produced in a particular circuit.

Next comes the integrator R5C7, after which crescent-shaped relaxation oscillations are obtained. The authors labeled this waveform a sawtooth or ramp, but it's more like shark fins.

After the second similar integrator, R6C8, a hybrid of a triangle and a sine wave is created: the tops are rounded, but the inclined sections are almost linear.

And finally, after the transistor stage on Q2, shunted by capacitor C9, we get an excellent approximation of a sinusoid. Resistor R8 provides base bias to Q2.

So we've seen what capacitors, resistors, and a transistor do to an electrical signal, and we learned how to build a simple generator with recognizable waveforms that can be used to study distortions in electrical circuits.

It is not that difficult to assemble a proper function generator on a special microcircuit. Still, it will definitely have more functions and better signal quality.

Professional-grade devices are, of course, more advanced, but they have a much higher price and substantially bigger dimensions. Unlike the three simple generators we've assembled and tested today, not every electronics enthusiast can afford them.